specMACS cloud geometry

In the following, an example of how to use the specMACS cloud geometry dataset will be shown. The cloud geometry is retrieved by a stereographic feature matching method described by Kölling et al. (2019). The algorithm is applied to the data of the two polarization resolving cameras of the instrument covering a large combined field of view of about \(\pm 45° \times \pm 59°\) (along track \(\times\) across track) (Pörtge et al., 2023). It is important to mention that no points found does not necessarily mean that no cloud has been observed as this can also happen if the cloud lacks in contrasts or due to a bad tracking of features.

Open dataset

The cloud geometry data were calculated for each of the flight segments flown by HALO seperately, thus data access will be per segment_id. The flight segmentation can be found in the respective github repository. In this example, we’ll have a look at the cloud geometry of the straight leg segment HALO-0205_sl1 flown on 2020-02-05. If you don’t know your favourite flight segment already or want to query or loop over multiple segments, please have a look at flight segmentation usage.

import eurec4a

segment_id = "HALO-0205_sl1"
cat = eurec4a.get_intake_catalog()
ds = cat.HALO.specMACS.cloud_geometry[segment_id].to_dask()
ds

/home/runner/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/intake_xarray/base.py:21: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  'dims': dict(self._ds.dims),

<xarray.Dataset> Size: 220MB
Dimensions:             (sample: 2392497, v: 3)
Dimensions without coordinates: sample, v
Data variables:
    time                (sample) datetime64[ns] 19MB ...
    lat                 (sample) float64 19MB ...
    lon                 (sample) float64 19MB ...
    height              (sample) float64 19MB ...
    height_above_geoid  (sample) float64 19MB ...
    loc                 (sample, v) float64 57MB ...
    viewpoint           (sample, v) float64 57MB ...
    max_misspointing    (sample) float32 10MB ...
Attributes:
    _NCProperties:                   version=2,netcdf=4.7.3,hdf5=1.10.4
    title:                           Stereographic retrieved cloud geometry b...
    institution:                     Meteorological Institut, Ludwig-Maximili...
    source:                          specMACS polcameras
    history:                         Created 2023-05-13T18:57:20
    references:                      Kölling, T., Zinner, T., and Mayer, B.: ...
    comment:                         This dataset contains stereographically ...
    contact:                         Lea Volkmer, L.Volkmer@physik.uni-muench...
    DODS_EXTRA.Unlimited_Dimension:  sample

xarray.Dataset

• Dimensions:
  • sample: 2392497
  • v: 3
• Coordinates: (0)
• Data variables: (8)
  • time
    (sample)
    datetime64[ns]
    ...

    long_name :

    time

    _ChunkSizes :

    512

    [2392497 values with dtype=datetime64[ns]]

  • lat
    (sample)
    float64
    ...

    units :

    degree_north

    long_name :

    latitude in WGS84

    _ChunkSizes :

    512

    [2392497 values with dtype=float64]

  • lon
    (sample)
    float64
    ...

    units :

    degree_east

    long_name :

    longitude in WGS84

    _ChunkSizes :

    512

    [2392497 values with dtype=float64]

  • height
    (sample)
    float64
    ...

    units :

    m

    long_name :

    height above WGS84

    _ChunkSizes :

    512

    [2392497 values with dtype=float64]

  • height_above_geoid
    (sample)
    float64
    ...

    units :

    m

    long_name :

    height above geoid/seasurface in meter

    _ChunkSizes :

    512

    [2392497 values with dtype=float64]

  • loc
    (sample, v)
    float64
    ...

    units :

    m

    long_name :

    location in cartesian reference frame at 13.1°N, -57.4°E

    _ChunkSizes :

    [1 3]

    [7177491 values with dtype=float64]

  • viewpoint
    (sample, v)
    float64
    ...

    long_name :

    camera location in cartesian reference frame at 13.1°N, -57.4°E

    units :

    m

    _ChunkSizes :

    [1 3]

    [7177491 values with dtype=float64]

  • max_misspointing
    (sample)
    float32
    ...

    units :

    m

    long_name :

    maximum misspointing from stereographic reconstruction

    _ChunkSizes :

    1024

    [2392497 values with dtype=float32]

• Indexes: (0)
• Attributes: (9)

  _NCProperties :

  version=2,netcdf=4.7.3,hdf5=1.10.4

  title :

  Stereographic retrieved cloud geometry based on Kölling et al 2019.

  institution :

  Meteorological Institut, Ludwig-Maximilians-University Munich

  source :

  specMACS polcameras

  history :

  Created 2023-05-13T18:57:20

  references :

  Kölling, T., Zinner, T., and Mayer, B.: Aircraft-based stereographic reconstruction of 3-D cloud geometry, Atmos. Meas. Tech., 12, 1155–1166, https://doi.org/10.5194/amt-12-1155-2019, 2019.

  comment :

  This dataset contains stereographically derived points on the cloud surfaces observed by the two polarization resolving cameras of specMACS. As the algorithm is based on feature matching due to contrast gradients, it does not have to mean that there is no cloud if no points are identified. This dataset is based on the camera calibration and orientation defined in https://gitlab.lrz.de/ls-mayer/mounttrees, commit b'00e719084b3e33c727046e835d2a59872752a39e'

  contact :

  Lea Volkmer, L.Volkmer@physik.uni-muenchen.de

  DODS_EXTRA.Unlimited_Dimension :

  sample

Simple plots

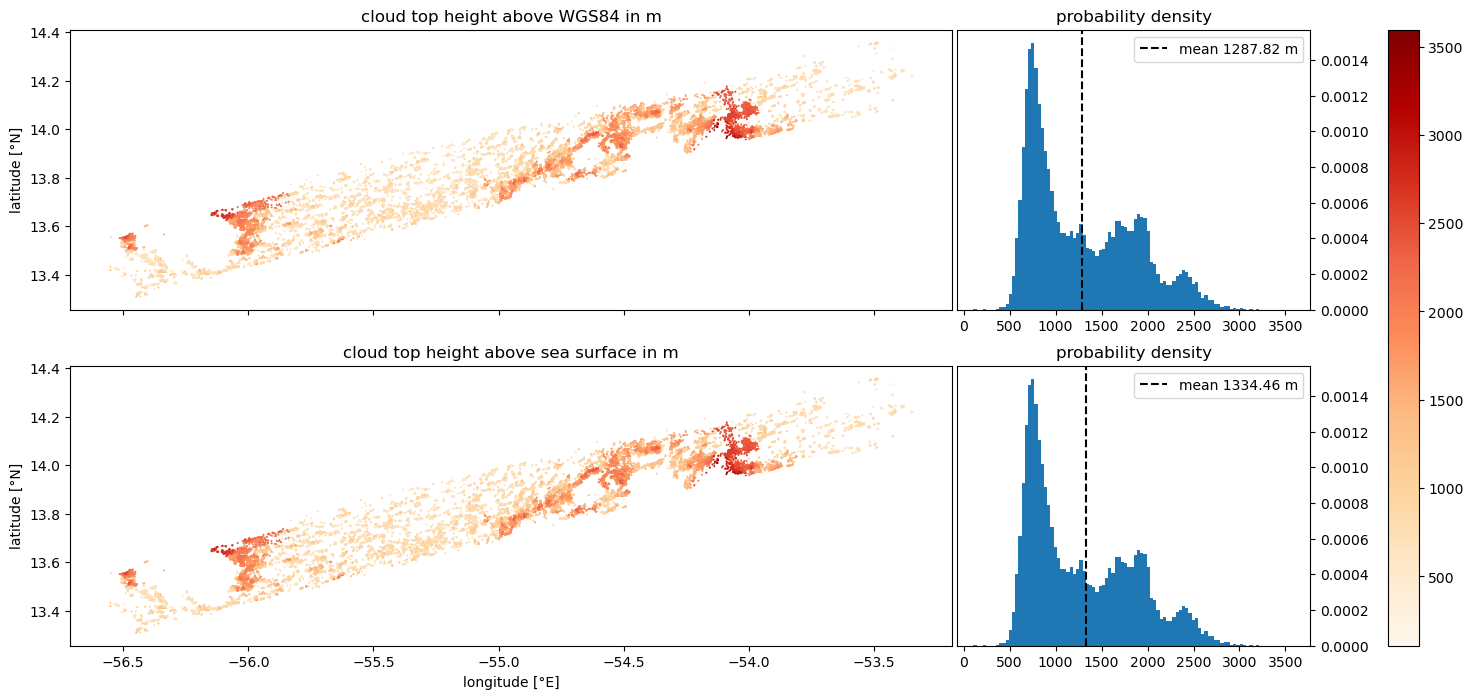
We will start to do some first simple scatter plots of the cloud top heights (CTH). There are two CTH variables in the dataset: A normal ‘height’ variable and a variable called ‘height_above_geoid’. The first is defined with respect to the WGS84 ellipsoid and the second with respect to the EGM2008 geoid. Although there is not a large difference between both in the EUREC4A area, we will exemplarily plot both.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable

We’ll select only every 100th data point for a quick overview.

Important

Depending on the clouds there might be a lot of points in the dataset or not such that this step might be useful or not.

ds_sel = ds.isel(sample=slice(0, None, 100))

load the data variables

lat = ds_sel['lat'].values
lon = ds_sel['lon'].values
height = ds_sel['height'].values
height_above_geoid = ds_sel['height_above_geoid'].values

cmap = 'OrRd'
vmin = np.min([height, height_above_geoid])
vmax = np.max([height, height_above_geoid])

fig, axs = plt.subplots(nrows=2, ncols=1, figsize=(20, 8), sharex=True)
for ax, var, ref in zip(axs, [height, height_above_geoid], ["WGS84", "sea surface"]):
    sm = ax.scatter(lon, lat, c=var, marker='o', s=2, edgecolor=None, linewidth=0, vmin=vmin, vmax=vmax, cmap=cmap)
    ax.set_title(f'cloud top height above {ref} in m')
    ax.set_ylabel('latitude [°N]')
    divider = make_axes_locatable(ax)
    ax2 = divider.append_axes('right', size='40%', pad=0.05)
    ax2.hist(height, bins=100, range=(vmin, vmax), density=True)
    ax2.set_title('probability density')
    ax2.yaxis.tick_right()
    ax2.axvline(np.mean(var), linestyle='dashed', color='k', label='mean {:.2f} m'.format(np.mean(var)))
    ax2.legend()

axs[1].set_xlabel('longitude [°E]')
plt.colorbar(sm, ax=axs)
None

Make a 3D plot

As the stereo points are points on the cloud surface located in 3D space, we can also do a 3D plot. We will use a few different viewing settings, which can also be individually adjusted using the elev and azim arguments of the ax.view_init setting.

import matplotlib.ticker as ticker

settings for plots

markersize = 0.1
cmap = 'viridis' #colormap
vmin = np.min(height)
vmax = np.max(height)

fig, axs = plt.subplots(2, 2, figsize=(14,12), subplot_kw=dict(projection='3d'))

for ax in axs.ravel():
    sm = ax.scatter(lon, lat, height, c=height, marker='o', vmin=vmin, vmax=vmax, cmap=cmap, s=markersize, linewidths=None, edgecolors=None)

ax = axs[0,0]
ax.set_xlabel('longitude [°E]', labelpad=6.0)
ax.set_ylabel('latitude [°N]', labelpad=6.0)
ax.set_zlabel('height above WGS84 [m]', labelpad=6.0)
ax.view_init(elev=None, azim=None)
ax.set_title('3D stereo plot', y=1.02)

ax = axs[0,1]
ax.set_ylabel('latitude [°N]', labelpad=6.0)
ax.set_zlabel('height above WGS84 [m]', labelpad=6.0)
ax.view_init(elev=0, azim=0)
ax.set_title('latitude-height plane', y=1.02)
ax.xaxis.set_major_locator(ticker.NullLocator())

ax = axs[1,0]
ax.set_xlabel('longitude [°E]', labelpad=4.0)
ax.set_ylabel('latitude [°N]', labelpad=6.0)
ax.view_init(elev=90, azim=-90)
ax.set_title('longitude-latitude plane', y=1.02)
ax.zaxis.set_major_locator(ticker.NullLocator())

ax = axs[1,1]
ax.set_xlabel('longitude [°E]', labelpad=6.0)
ax.set_zlabel('height above WGS84 [m]', labelpad=10.0)
ax.view_init(elev=0, azim=-90)
ax.set_title('longitude-height plane', y=1.02)
ax.yaxis.set_major_locator(ticker.NullLocator())

plt.subplots_adjust(bottom=0.1, right=0.9)
cax = plt.axes([0.95, 0.15, 0.05, 0.7])
fig.colorbar(sm, cax=cax, label='height above WGS84 [m]', fraction=0.02, shrink=2.0, aspect=40)
None

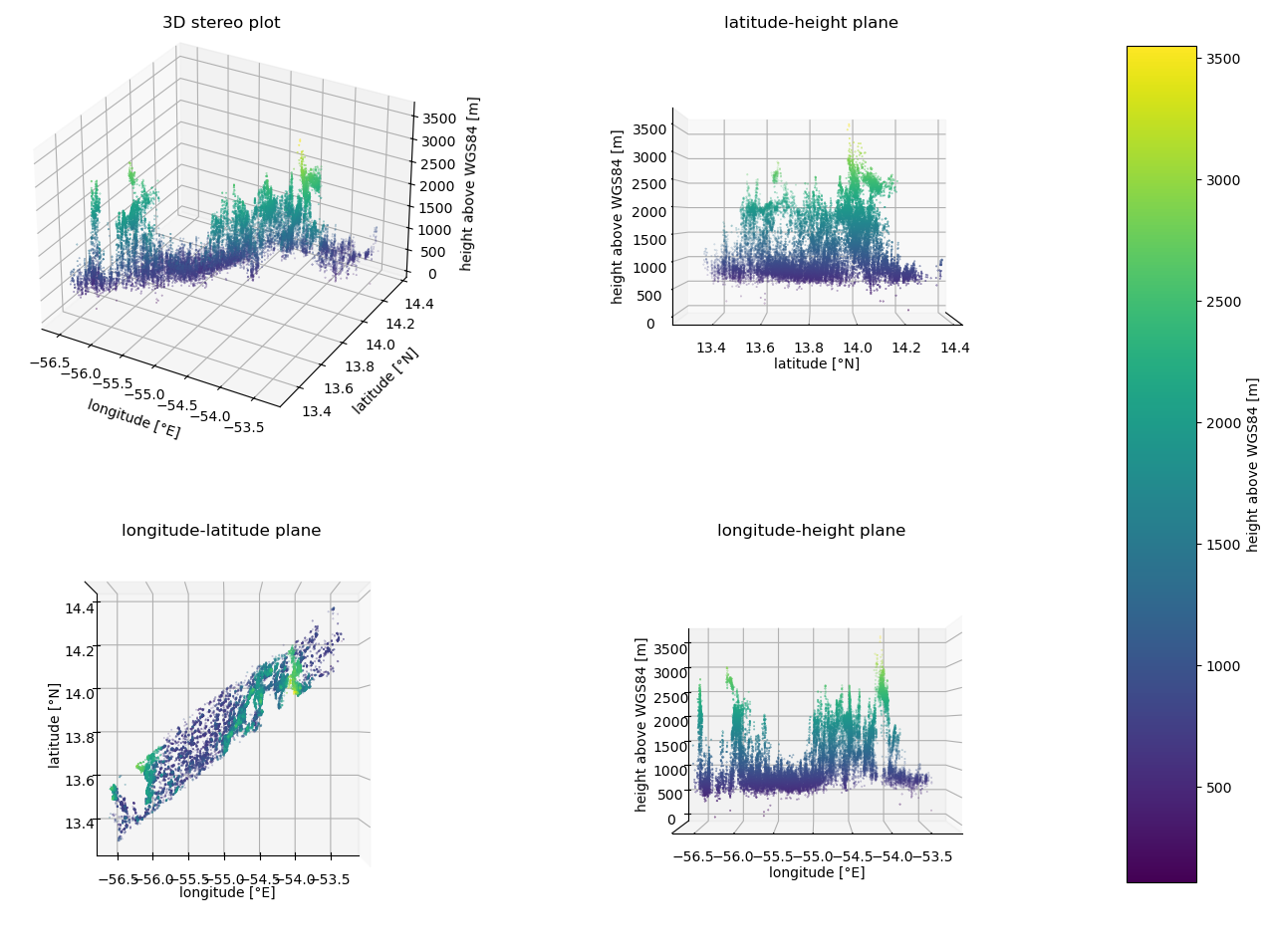
The 3D plots show the scene from different perspectives. It can be seen that the tracking algorithm finds points in both cloud layers down to a base height of approximately 1000m. Below, there are also some points which are probably outliers due to some wrong identifications.

Project points to specMACS measurements

We will start to project the points found from the stereographic reconstruction to pre-rendered specMACS tile maps which can be found here. To make them available to cartopy, we need a little helper class specMACSPTiles, which mainly takes care of making unavailable tiles transparent (these are outside the viewing range of the instrument).

Show code cell content Hide code cell content

from cartopy.io.img_tiles import GoogleWTS
from PIL import Image

class specMACSPTiles(GoogleWTS):
    def __init__(self, flight_segment_id):
        super().__init__(desired_tile_form="RGBA")
        self.flight_segment_id = flight_segment_id
        self.empty_tile = Image.fromarray(np.full((256, 256, 4), (255, 255, 255, 0), dtype=np.uint8))

    def get_image(self, tile):
        from io import BytesIO
        from urllib.request import urlopen, Request, HTTPError, URLError

        url = self._image_url(tile)
        try:
            request = Request(url)
            fh = urlopen(request)
            im_data = BytesIO(fh.read())
            fh.close()
            img = Image.open(im_data)

        except (HTTPError, URLError) as err:
            img = self.empty_tile

        img = img.convert(self.desired_tile_form)
        return img, self.tileextent(tile), 'lower'

    def _image_url(self, tile):
        x, y, z = tile
        return f"https://macsserver.physik.uni-muenchen.de/campaigns/EUREC4A/maps/tiles/{self.flight_segment_id}/{z}/{x}/{y}.png"

We can now get the tile map for our selected flight segment:

specmacs = specMACSPTiles(segment_id)

Get vmin and vmax using quantiles such that outliers will not influence the colorbar too much:

q = 0.01
vmin, vmax = np.quantile(height, [q, 1-q])
cmap = 'OrRd'

import cartopy.crs as ccrs

fig, axes = plt.subplots(1, 2, figsize=(16, 8), constrained_layout=True, subplot_kw={"projection": ccrs.PlateCarree()})
for ax in axes:
    ax.set_extent([np.floor(np.min(lon)), np.ceil(np.max(lon)), np.floor(np.min(lat)), np.ceil(np.max(lat))], crs=ccrs.PlateCarree())
    ax.add_image(specmacs, 8)  # the number is an integer and represents the detail level. It is logarithmic, small values are coarse, large values are fine.
    ax.set_axis_off()
im = ax.scatter(lon, lat, c=height, marker="o", s=0.4, edgecolor=None, linewidth=0, vmin=vmin, vmax=vmax, cmap=cmap)
fig.colorbar(im, label='height above WGS84 [m]', extend='both', shrink=0.4)
None

Error in callback <function _draw_all_if_interactive at 0x7f8f37ef7560> (for post_execute), with arguments args (),kwargs {}:

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/pyplot.py:279, in _draw_all_if_interactive()
    277 def _draw_all_if_interactive() -> None:
    278     if matplotlib.is_interactive():
--> 279         draw_all()

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/_pylab_helpers.py:131, in Gcf.draw_all(cls, force)
    129 for manager in cls.get_all_fig_managers():
    130     if force or manager.canvas.figure.stale:
--> 131         manager.canvas.draw_idle()

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/backend_bases.py:1891, in FigureCanvasBase.draw_idle(self, *args, **kwargs)
   1889 if not self._is_idle_drawing:
   1890     with self._idle_draw_cntx():
-> 1891         self.draw(*args, **kwargs)

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/backends/backend_agg.py:382, in FigureCanvasAgg.draw(self)
    379 # Acquire a lock on the shared font cache.
    380 with (self.toolbar._wait_cursor_for_draw_cm() if self.toolbar
    381       else nullcontext()):
--> 382     self.figure.draw(self.renderer)
    383     # A GUI class may be need to update a window using this draw, so
    384     # don't forget to call the superclass.
    385     super().draw()

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/figure.py:3257, in Figure.draw(self, renderer)
   3254             # ValueError can occur when resizing a window.
   3256     self.patch.draw(renderer)
-> 3257     mimage._draw_list_compositing_images(
   3258         renderer, self, artists, self.suppressComposite)
   3260     renderer.close_group('figure')
   3261 finally:

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/cartopy/mpl/geoaxes.py:517, in GeoAxes.draw(self, renderer, **kwargs)
    515 if not self._done_img_factory:
    516     for factory, factory_args, factory_kwargs in self.img_factories:
--> 517         img, extent, origin = factory.image_for_domain(
    518             self._get_extent_geom(factory.crs), factory_args[0])
    519         self.imshow(img, extent=extent, origin=origin,
    520                     transform=factory.crs, *factory_args[1:],
    521                     **factory_kwargs)
    522 self._done_img_factory = True

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/cartopy/io/img_tiles.py:98, in GoogleWTS.image_for_domain(self, target_domain, target_z)
     95         except OSError:
     96             pass
---> 98 img, extent, origin = _merge_tiles(tiles)
     99 return img, extent, origin

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/cartopy/io/img_tiles.py:684, in _merge_tiles(tiles)
    682 """Return a single image, merging the given images."""
    683 if not tiles:
--> 684     raise ValueError('A non-empty list of tiles should '
    685                      'be provided to merge.')
    686 xset = [set(x) for i, x, y, _ in tiles]
    687 yset = [set(y) for i, x, y, _ in tiles]

ValueError: A non-empty list of tiles should be provided to merge.

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/IPython/core/formatters.py:402, in BaseFormatter.__call__(self, obj)
    400     pass
    401 else:
--> 402     return printer(obj)
    403 # Finally look for special method names
    404 method = get_real_method(obj, self.print_method)

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/IPython/core/pylabtools.py:170, in print_figure(fig, fmt, bbox_inches, base64, **kwargs)
    167     from matplotlib.backend_bases import FigureCanvasBase
    168     FigureCanvasBase(fig)
--> 170 fig.canvas.print_figure(bytes_io, **kw)
    171 data = bytes_io.getvalue()
    172 if fmt == 'svg':

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/backend_bases.py:2155, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2152     # we do this instead of `self.figure.draw_without_rendering`
   2153     # so that we can inject the orientation
   2154     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2155         self.figure.draw(renderer)
   2156 if bbox_inches:
   2157     if bbox_inches == "tight":

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/figure.py:3257, in Figure.draw(self, renderer)
   3254             # ValueError can occur when resizing a window.
   3256     self.patch.draw(renderer)
-> 3257     mimage._draw_list_compositing_images(
   3258         renderer, self, artists, self.suppressComposite)
   3260     renderer.close_group('figure')
   3261 finally:

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/cartopy/mpl/geoaxes.py:517, in GeoAxes.draw(self, renderer, **kwargs)
    515 if not self._done_img_factory:
    516     for factory, factory_args, factory_kwargs in self.img_factories:
--> 517         img, extent, origin = factory.image_for_domain(
    518             self._get_extent_geom(factory.crs), factory_args[0])
    519         self.imshow(img, extent=extent, origin=origin,
    520                     transform=factory.crs, *factory_args[1:],
    521                     **factory_kwargs)
    522 self._done_img_factory = True

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/cartopy/io/img_tiles.py:98, in GoogleWTS.image_for_domain(self, target_domain, target_z)
     95         except OSError:
     96             pass
---> 98 img, extent, origin = _merge_tiles(tiles)
     99 return img, extent, origin

File ~/miniconda3/envs/how_to_eurec4a/lib/python3.13/site-packages/cartopy/io/img_tiles.py:684, in _merge_tiles(tiles)
    682 """Return a single image, merging the given images."""
    683 if not tiles:
--> 684     raise ValueError('A non-empty list of tiles should '
    685                      'be provided to merge.')
    686 xset = [set(x) for i, x, y, _ in tiles]
    687 yset = [set(y) for i, x, y, _ in tiles]

ValueError: A non-empty list of tiles should be provided to merge.

<Figure size 1600x800 with 3 Axes>

The projection of the points to the specMACS map on the right shows that most of the clouds, in particular the small cumulus clouds are well identified and located by the stereographic reconstruction method. The only exception is the higher and thicker cloud toward the end of the leg. This cloud lacks contrasts such that only its edges are identified well by the tracking algorithm.